

Mit Knoten werden Orte auf einer Karte beschrieben. Man kann sich Knoten als Bahnhöfe vorstellen.
Im Bild sieht man einen grauen Knoten A.

Mit Kanten werden Verbindungen zwischen Orten beschrieben. Man kann sie sich als Streckenabschnitte (Stationen) vorstellen.
Im Bild sieht man eine graue Kante zwischen zwei grauen Knoten B und C.

Ein Graph besteht aus Knoten und Kanten und wird dazu benutzt, Probleme mathematisch zu formulieren. Der Graph links im Bild besteht aus 7 Knoten und 7 Kanten.

Knoten B ist der Nachbar von Knoten C (und umgekehrt), wenn B und C durch eine Kante verbunden sind. B und C heißen dann benachbart.

Ein Weg ist ein Kantenzug, bei dem jeder Knoten nur einmal vorkommt.

Ein Kreis ist ein Weg mit gleichem Anfangs- und Endknoten.

Ein Graph wird vollständig genannt, wenn von jedem seiner Knoten zu jedem anderen eine Kante verläuft.
Im Bild sieht man den K5. Er spielt in der Graphentheorie eine wichtige Rolle. Allgemein wird der vollständige Graph mit n Knoten mit "Kn" bezeichnet.

Ein Graph wird unzusammenhängend genannt, wenn es zwei Knoten gibt, zwischen denen kein Weg existiert. Das Berliner U+S-Bahn-Netz ist zusammenhängend, nicht jedoch das MetroNetz. Vom Rathaus Spandau kann man mit dem Metro-Bus nur Spandauer Stationen erreichen, die Philharmonie aber nicht.
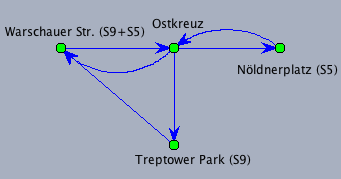
Wenn die Kanten eines Graphen eine Richtung haben, spricht man von einem gerichteten Graphen. Im Berliner S-Bahn-Netz fährt die S9 Richtung Westen direkt von Treptower Park nach Warschauer Str., in Richtung Osten fährt sie von Warschauer Str. über Ostkreuz nach Treptower Park.
Wenn keine Kante des Graphen gerichtet ist, spricht man von einem ungerichteten Graphen.

Ein Graph mit Kantengewichten wird gewichteter Graph genannt. Die Kantengewichte geben in unserem U+S-Bahn-Netz-Beispiel die Fahrtdauer zwischen, bzw. Wartedauer auf den Bahnhöfen an.
©2005 Anne Geschke, Ulrich Kortenkamp, Dirk Materlik. Technische Universität Berlin, DFG-Forschungszentrum Matheon