GeoProof

1- Introduction

Dynamic geometry software and computer algebra software are the most widely used software for mathematics in education. Dynamic geometry software allow the user to create geometric constructions and to animate these constructions by dragging the free objects. All the depending objects are updated in real time. Computer algebra software allows to perform computations. As the proving activity is central in mathematics, it is surprising that most software systems which are in widespread use to teach mathematics can not deal with this activity. Software which are specialized in proofs do exist, they are called proof assistants. Adapting proof assistants to be used in the classroom is an active research field [1].

The education community has studied the impact of the use of Dynamic Geometry Software (DGS) on the proving activity [2,3].
DGS are mainly used for two activities:

• to make the student create geometric constructions;
• to make the student explore the figure, invent conjectures and check facts. 
  

We believe that these software systems should also be used to help the student in the proving activity itself. Work has been performed in this direction and several DGS with proof related features have been produced. These systems can be roughly classified into two categories:

1. the systems which permit to build proofs;
2. the systems which permit to check facts using an automated theorem prover. 
   

The Geometry Tutor [4], Mentoniezh [5], Defi [6], Chypre [7], Cabri-Euclide [8], GEOLOG [9], Geometrix [10] and Baghera systems belongs to the first category. Using these systems the student can produce proofs interactively using a set of known theorems. In most of these systems the student can not invent a proof very different from what the program had pre-computed using automated theorem proving methods. As far as we know, the exception is Cabri-Euclide which contains a small formal system and therefore gives more freedom to the student. Baghera includes also e-learning features, such as task management and network communication between teachers and their students.


The work closest to ours consists in the software GeoView by Yves Bertot, Frédérique Guilhot and Loïc Pottier [19]. The GeoView software provides a visualization tool for some formal geometric statements using an off-the-shelf DGS and the PCoq user interface for Coq.

We developed a software called GeoProof, whose goal is to build a bridge between the world of proof assistants and dynamic geometry.
GeoProof is a free and open source dynamic geometry software distributed under the terms of the GPL Version 2. It is written in Ocaml using lablgtk2. We wrote GeoProof using these tools to ease the future integration within the Coq graphical user interface CoqIDE.

 The difference between our approach and the other systems we have cited (except GeoView) is that we use of a general purpose proof assistant and combine interactive and automated theorem proving. The use of a proof assistant provides a very high level of confidence in the proofs generated. Note that this is important because as highlighted by J. Escribano, M. Abanades, J. Valcarce and F. Botana [18], the use of an incorrect method such as the numerical approach used by Cabri can lead to errors. During our formalisation of the Area Method in Coq [21] we also found some small errors in some of the lemmas proposed by the authors of the method. The difference between our system and GeoView is that communication with Coq goes in the other direction, Geoview allow to display the figure corresponding to a Coq statement about geometry, GeoProof allows to create a statement corresponding to a figure. GeoProof also helps proving the existence of an object constructed during a proof.

GeoProof allows to :

• construct a geometric figure, 
• animate it by dragging free points,
• study a conjecture using dynamic labels,
• prove a conjecture using an embedded automatic theorem prover,
• prove a conjecture automatically using the Coq proof assistant,
• prove a conjecture interactively using the Coq proof assistant.

In depth explanations about the motivations, the implementation, the semantics of the theorems associated to a figure and how to deal with degenerated cases is given in the paper [20]. The description of the formalisation of the area method in Coq is given in [21]. Here we take advantage of the medium to demonstrate the concrete use of the system using videos; this page is a multimedia complement for [20]. First, we give a quick overview of the system, then we present a case study and treat it using GeoProof.

2- A quick overview of the system

The GeoProof graphical user interface is standard for a dynamic geometry software system. The main window contains three tabs: the main interactive window, the description of the figure in natural language, the preview of an output of the figure  as .svg file. The toolbars contains buttons to: create new geometric objects, create dynamic labels to test predicates, change the display of the figure... The originality of GeoProof resides in: The proof related features described in the next sections. The fact that all computations are performed using arbitrary precision. This ensure that the figure displayed really corresponds to a correct approximation of the perfect figure.

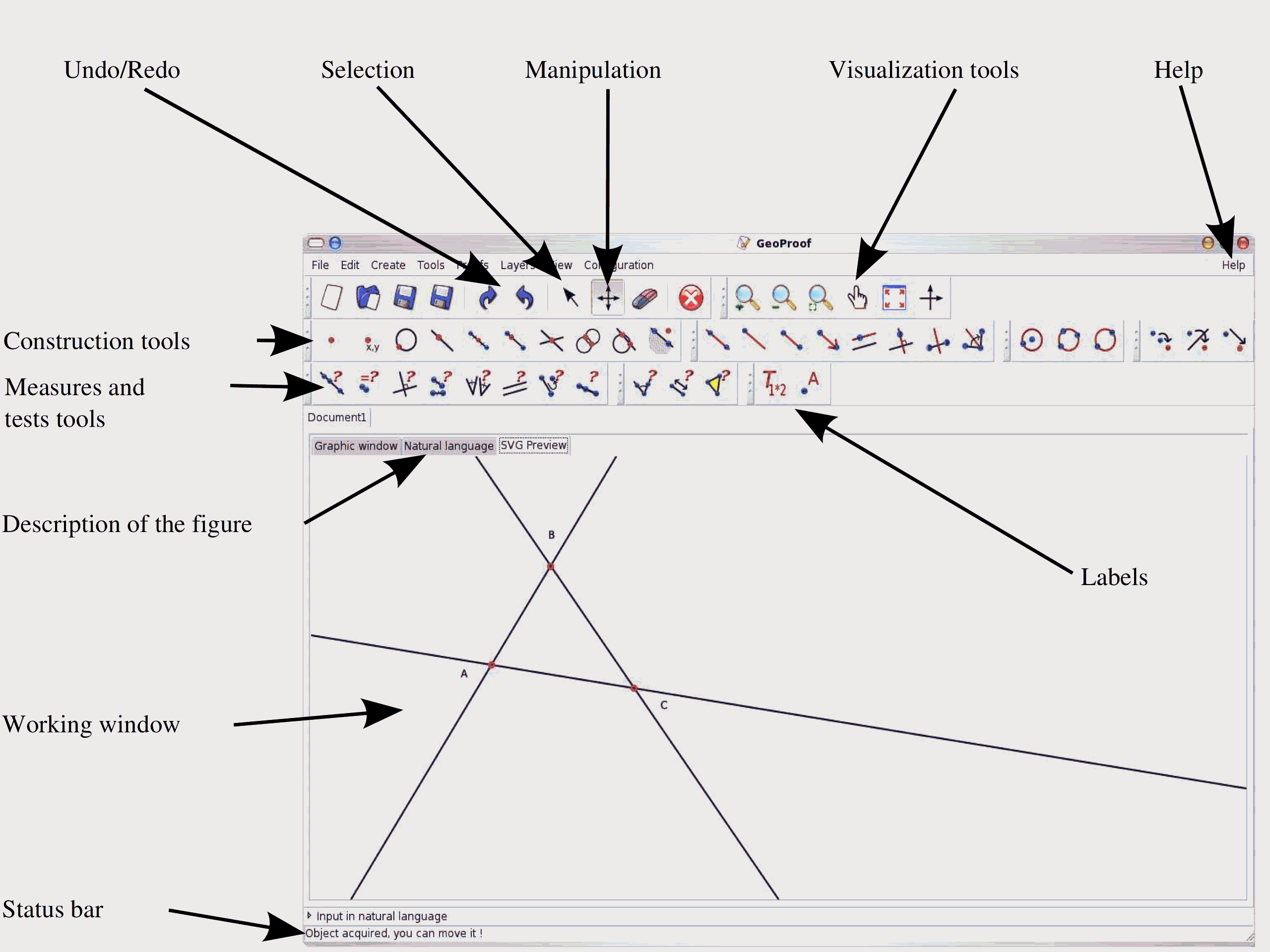2.1 Dynamic labels

Dynamic labels are fragments of text which represent an expression. The expressions can depend on other objects and are evaluated dynamically. The dynamic labels can contain arithmetic expressions (+ - * /), mathematical functions (sin, cos, tan, sqrt, min, max...), logic connectives, strings, local definitions, if statements...
As all computations are performed using arbitrary precision the result does not suffer from approximations.
For instance if we try to compute sin(10²²) we get the correct answer (-0.852200849) whereas other software systems produce various results as shown on table on the right.

The following video demonstrate the use of labels with dynamic placeholders. This video shows how labels can be used to display first a distance, second the signed area of a triangle and finally to test if a point is on the left of a line using a conditional expression.





 

3- A case study : the midpoint theorem

In this section we study an example using the different features of GeoProof. Let's study the midpoint theorem :

The midpoint theorem : Let ABC be a triangle and let D and E be the midpoints of AC and BC respectively. Then the line DE is parallel to the base AB.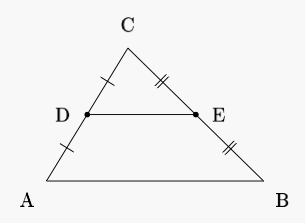

The user can first construct the figure using GeoProof, then try to invent a conjecture.  Here, the conjecture is obvious : the line DE is parallel to the line AB. Then the user can explore the figure interactively to test empirically if the conjecture is true. This can be done thanks to the labels with dynamic placeholders.

3.1- Check conjectures using labels with dynamic placeholders

The following video show the use a label to empirically test a conjecture. The first show the construction of the figure and then we create a dynamic label using one of the tool to test predicates. GeoProof provide direct access to tools to test some predicates (collinear, perpendicular, parallel, same length, same angle measure, left-turn, between, equality). Note that buttons are just shortcuts which create labels containing a dynamic placeholder as shown on the video.

3.2- Automatic proof using the embedded theorem prover

In the following video we demonstrate how GeoProof can be used to check the midpoint theorem using the embedded theorem prover. The windows is splited into two sections. The first one contains the hypotheses and the second one the goal. When the proving window is opened the initial list of hypotheses corresponds to the current figure. is_midpoint D A B means that D is the midpoint of the segment [AB].
GeoProof first check in the background if it is possible to prove false from the hypotheses. This test is performed to warn the user in case the assumptions are contradictory. This case can occur if the user tries to build an object which do not exist whatever are the positions of the free points.

3.3- Automatic proof using Coq

In the following video we demonstrate how GeoProof can be used to check the midpoint theorem using the Coq proof assistant. We first construct the figure. Then we declare that we want to perform the proof using Coq. At this step we have to choose between two developments about geometry in Coq. The first one is our formalisation of the Area Method, the second one is the formalisation of high-school geometry by Frédérique Guilhot. The specifications corresponding to the current figure are translated into Coq's syntax. We create a dynamic label to test if the two lines are parallel. A right click on this label allows to translate this predicate into Coq syntax and to start proving the conjecture. Note that the proving command appears in the contextual menu of label only when the type of the dynamic placeholder of the label is bool. Finally, we decide to prove the theorem automatically using the Area Method.

Conclusion

We have presented the system GeoProof, and how it can be used to prove automatically some theorems and to ease the creation of a formal statement which is then proved interactively using Coq. Proving theorems using Coq is accessible only to expert users of the system and therefore can not be used in the education context. Hence, the next research subject consists in developing tools to ease the proving process by hiding to the user the underlying complexity of the proof assistant. To achieve this goal we will have to provide to user a good presentation of the current state of the proof together with a way to apply a theorem graphically.

Bibliography

1. Günther Mayrhofer, Susanne Saminger and Wolfgang Windsteiger, CreaComp: Experimental Formal Mathematics for the Classroom, In Proceedings of ICTMT8, Eva Milkova (ed.), 2007.
2. Oleksiy Yevdokimov, About a constructivist approach for stimulating students' thinking to produce conjectures and their proving in active learning of geometry, In Fourth Congress of the European Society for Research in Mathematics Education, 2004.
3. Fulvia Furinghetti and Paoloa Domingo, To produce conjectures and to prove them within a dynamic geometry environment: a case study, In Proceeding of Psychology of Mathematics 27th international Conference, pages 397-404, 2003.
4. John R. Anderson, C.F. Boyle and Gregg Yost, The Geometry Tutor, published in IJCAI Proceedings, pages 1-7, 1985.
5. Dominique Py, Reconnaissance de plan pour l'aide à la démonstration dans un tuteur intelligent de la géométrie, PhD thesis, Université de Rennes, 1990.
6. Ag-Almouloud, L'ordinateur, outil d'aide à l'apprentissage de la démonstration et de traitement de données didactiques, PhD thesis, Université de Rennes, 1992.
7. Philippe Bernat, Chypre: Un logiciel d'aide au raisonnement, Technical Report 10, IREM, 1993.
8. Vanda Luengo, Cabri-Euclide: Un micromonde de Preuve intégrant la réfutation, PhD thesis, Université Joseph Fourier, 1997.
9. Gerhard Holland, Geolog, 2002-2006.
10. Jacques Gressier, Geometrix, 1988-1998
11. Xian-Shan Gao and Qiang Lin, MMP/Geometer - a software package for automated geometry reasoning, In F. Winkler, editor, Proceedings of ADG 2002, Lecture Notes in Computer Science, pages 44-46. Springer-Verlag, 2002.
12. Xiao-Shan Gao, Geometry expert, software package, 2000.
13. Sean Wilson and Jacques Fleuriot, Combining dynamic geometry, automated geometry theorem proving and diagrammatic proofs, In ETAPS Satellite Workshop on User Interfaces for Theorem Provers (UITP), Edinburgh, 2005.
14. Predrag Janicic, Pedro Quaresma, System Description: GCLCprover + GeoThms, International Joint Conference on Automated Reasoning (IJCAR-2006), Furbach, Ulrich and Shankar, Natarajan, editors. Lecture Notes in Artificial Intelligence, volume 4130, pages 145-150, Springer-Verlag, 2006.
15. Ulrich Kortenkamp, Foundations of Dynamic Geometry, PhD thesis, ETH Zürich, 1999.
16. Jacob T. Schwartz, Probabilistic algorithms for verification of polynomial identities, In Symbolic and algebraic computation, volume 72 of Lecture Notes in Computer Science, pages 200-215, Marseille, 1979. Springer-Verlag.
17. Shang-Ching Chou, Xiao-Shan Gao, and Jing-Zhong Zhang, Automated generation of readable proofs with geometric invariants, theorem proving with full angle, Journal of Automated Reasoning 17:325--347, 1996.
18. J. Escribano, M. Abanades, J. Valcarce and F. Botana, On Using OpenMath for Representing Dynamic Geometry Constructions, In Proceedings of ADG 2006.
19. Yves Bertot, Frédérique Guilhot, and Loïc Pottier, Visualizing geometrical statements with GeoView, Electronic Notes in Theoretical Computer Science 103:49-65, September 2003.
20. Julien Narboux, A Graphical User Interface for Formal Proofs in Geometry, to appear in the Journal of Automated Reasoning [.pdf].
21. Julien Narboux, A Decision Procedure for Geometry in Coq, published in TPHOLs'04 proceedings [.pdf].