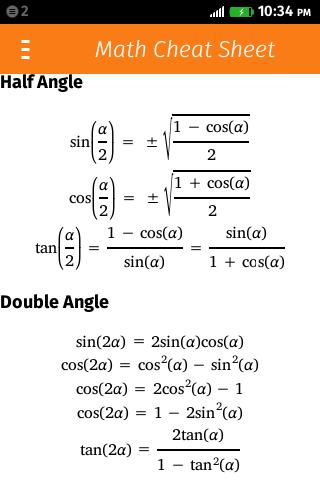
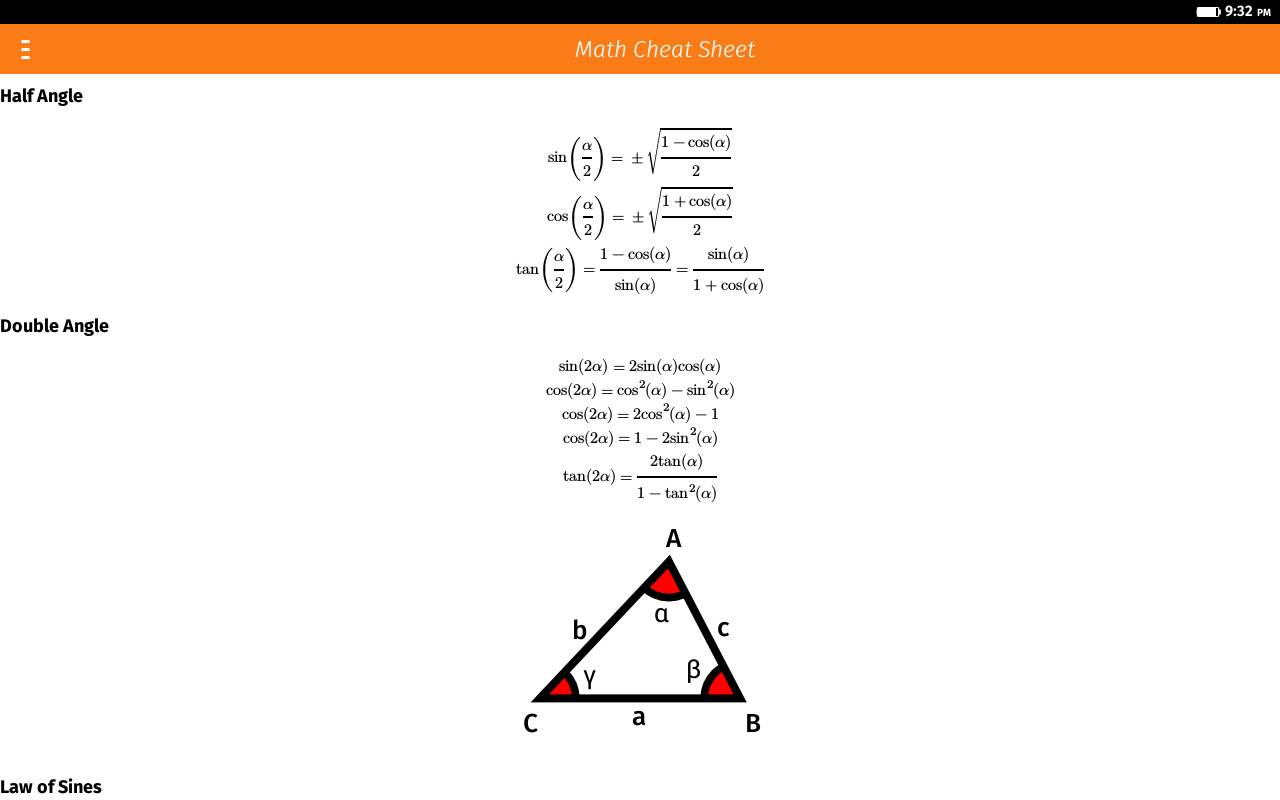
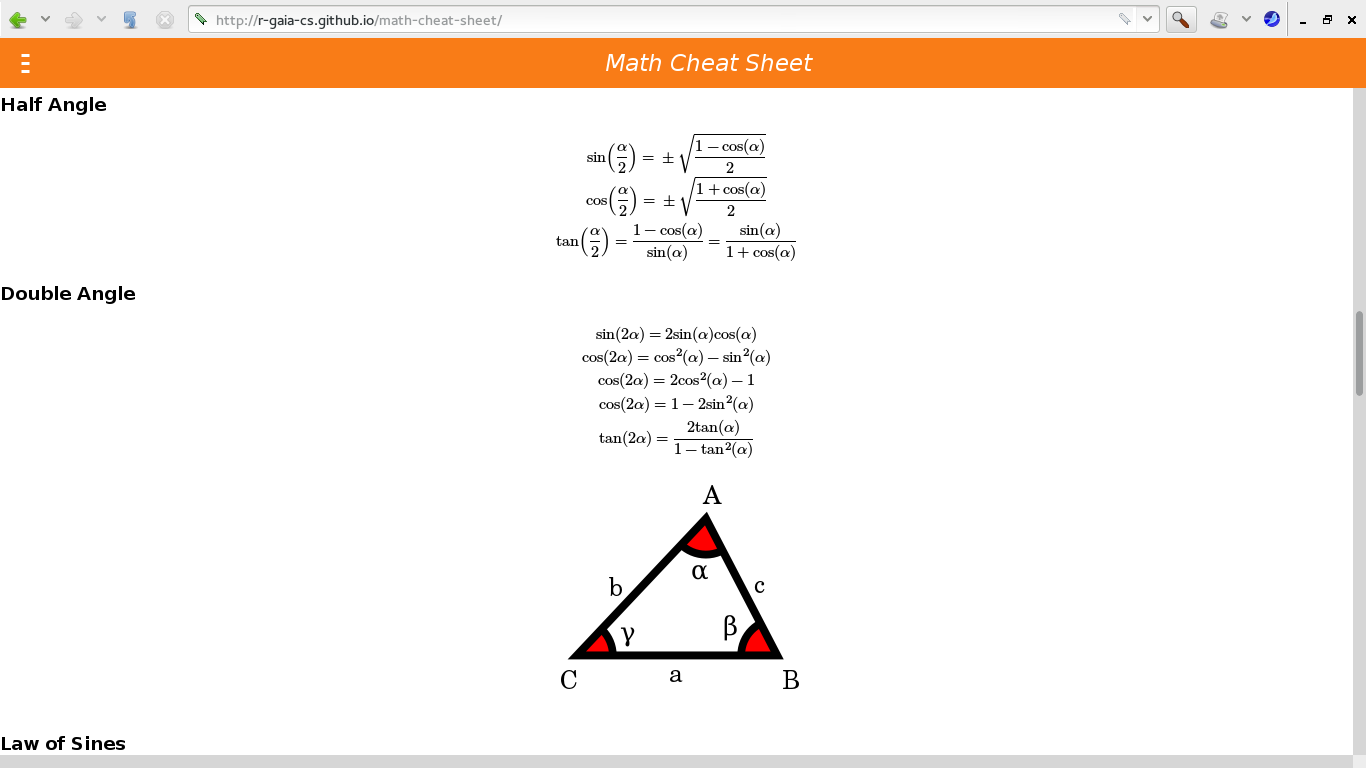
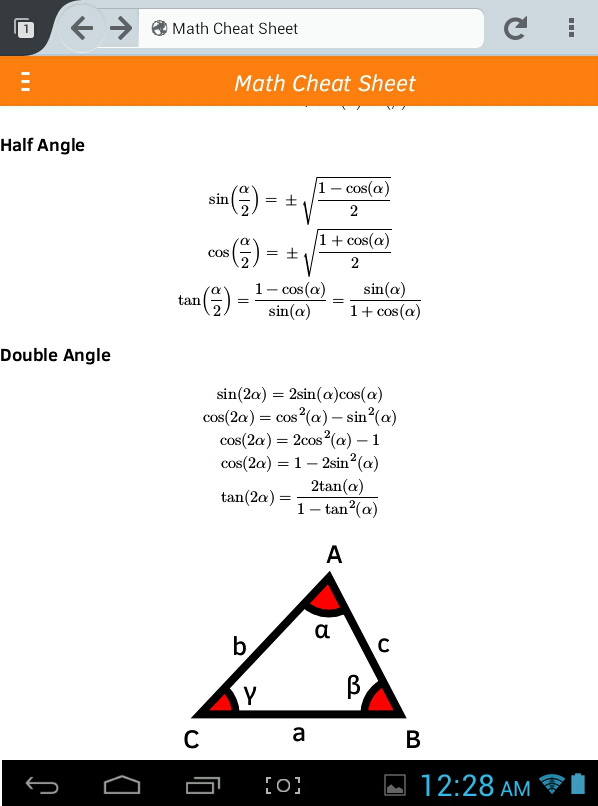
Firefox OS Web Apps for Science
 Raniere Silva and Frédéric Wang, MathUI2014, Coimbra, July 10th 2014
Raniere Silva and Frédéric Wang, MathUI2014, Coimbra, July 10th 2014
Raniere Silva and Frédéric Wang, dev-tech-mathml@lists.mozilla.org
 Raniere Silva and Frédéric Wang, MathUI2014, Coimbra, July 10th 2014
Raniere Silva and Frédéric Wang, MathUI2014, Coimbra, July 10th 2014


س = \frac{-ب \pm \sqrt{ب^٢ - ٤اج}}{٢ا}
<x-tex display="block">
\Gamma(t) =
\frac{1}{t} \prod_{n=1}^\infty
\frac{\left(1+\frac{1}{n}\right)^t}{1+\frac{t}{n}} =
\frac{e^{-\gamma t}}{t} \prod_{n=1}^\infty
\left(1 + \frac{t}{n}\right)^{-1} e^{\frac{t}{n}}
</x-tex>
| Packaged | Hosted |
|---|---|
|
|
{
"version": "1.0.0",
"name": "App",
"description": "App short description",
"launch_path": "/index.html",
"icons": {
"128": "/img/icon-128.png"
},
"developer": {
"name": "Your name or organization",
"url": "http://your-homepage-here.org"
},
"default_locale": "en"
}